By Mona Iehl
Sighs ripple through the room. Erasers scratch the paper, some pressing hard enough to tear right through. It was September, and a new teacher was guiding her fifth graders through this word problem:
Each pitcher of lemonade needs 5.11 ounces of fresh lemon juice. If Alana makes 10 pitchers of lemonade, how many ounces of fresh lemon juice will she need? Show your reasoning with pictures, numbers, or equations.
A few minutes earlier, she had read the directions from the teacher’s manual and displayed the curriculum’s provided slides on the SMARTboard. As soon as she finished, hands shot into the air. One especially flustered fifth grader in the back caught her eye.
“Do we have to show our work?” she asked, her voice half pleading.
“Yes,” the teacher replied, trying not to let her own frustration show. “We talk about this every day. It’s right there in the directions. It is so important to show your thinking. We have four minutes to work on this. Go ahead and get started, friends.”
Work time begins and students look busy at first, heads down and pencils moving. But upon closer examination, students’ papers showed their answer and little else. No labels, units, equations, diagrams or explanations. Just the answer, despite the teacher’s best effort.
What We’re Up Against
Sometimes it feels like no matter what we do, students resist showing their reasoning. When we force it, they scribble something, anything, just to meet the requirement. But this habit misses the whole point of mathematics: using strategies to problem solve and find a solution.
To empower our students to show their reasoning, a culture shift is needed. We need to stop treating “show your reasoning” as a final step and start treating it as the heart of how we do math.
However, as I dug into this in my own classroom and those of the teachers I coach, I learned that the real barrier wasn’t just instruction, it was also mindset. Here’s some of what I was up against:
- Students value being “right” and getting the correct answer over everything else. The emphasis in math is often on how many questions you got right or how many points you earned.
- Many students say there’s no time to show their thinking because they’ve been assigned so many problems to complete.
- And for most of them, math has always meant speed and answers – not slow thinking and strategy. Showing your reasoning was not part of what they saw valued in mathematics.
Getting students to show their reasoning isn’t about adding on more directions, it’s about shifting the notion of how we do math. Too often, “show your work” comes after students have solved the problem in their heads, as a formality to check a box. But when we believe that reasoning is the math, we teach students to record their thinking as they go, to make sense of the problem, communicate ideas, and prove their reasoning to allow others to learn from them.
This shift doesn’t start with a strategy or teacher move. It starts with our beliefs, and it shows up in the norms, routines, and expectations we build every day in our classrooms.
A Shift in What It Means to Do Math
The shift is about more than what students write on paper. It is about reimagining what it means to do math. In my own classroom, I shifted the focus to the process of doing mathematics. Like this: we honor students’ time, effort, and reasoning while they problem solve. We create a classroom culture that values students’ thinking, not just correctness. Our class time is used to share, discuss, analyze, and learn from each other’s ideas.
Although this may sound good, our beliefs and mindset must shift in order to bring the ages-old definition of “show your work” into a new light. There are 3 main beliefs that can help us and our students see showing your reasoning as the way we do math.
✻ Believe in the Process.
Put less emphasis on the answer and more on the process. That might feel uncomfortable at first. We’ve all grown up in a system that defines math as fast, rigid, and all about “getting it right.” But in truth, great mathematicians do slow math; the kind that involves pondering, reworking, and wondering.
In the real world, math is collaborative and complex. Engineers, doctors, and construction workers aren’t paid for their answers; they’re paid for the thinking that gets them there. Of course answers matter. But we must prioritize how students get there: their strategies, reasoning, and perseverance. Like the finish line of a race, the answer is a goal, but the learning happens in the miles before it.
✻ Believe in Student Voice.
It is a traditionally held belief that the best way to teach math is to show students what to do and then ask them to practice those steps to arrive at the answer. Memorizing and repeating are low levels of cognitive demand, and often lead to shallow understanding.
When we do all the talking and explaining, we rob students of the opportunity to think, explore, and make sense of the math for themselves. Instead, we must shift students’ thinking and voice to the center and assume the role of facilitating discussions about students’ thinking.
✻ Believe in Their Brilliance.
So often our curriculum scripts a narrow path: we model, they mimic, and we all race to the answer. But our classrooms are more diverse than a script allows for. We can create a classroom that allows students to come to the problem and utilize their expertise and natural curiosity to problem solve.
We must create a culture where students bring ALL of their expertise to the table. We start with problems, not steps, and let students reason through them. Whether it’s fractions, decimals, or linear equations, our students come with real world mathematical experiences that are essential to math class. They come with a natural curiosity and strengths we can tap into.
When we let students explore, observe them closely, and seek to understand their thinking first, everything shifts. We’re no longer gatekeeping concepts or holding off until we think everyone’s “ready.” We’re trusting students to engage, grapple, and grow, because they already have what it takes to begin.
How We Make Reasoning the Way We Do Math
#1 – Ask students to share their reasoning, not their answer. Start asking for students to describe their thinking, reasoning, and methods. Pay much less (or no) attention to the answer. Sometimes I like to get it out of the way immediately.
I might say something like, “The answer is 50.11 cups of water. Now, let’s talk about how we solved this problem. Tilly, will you share how you solved with us please? Tell us what you did and why you did it.” This approach puts the emphasis of the discussion on the reasoning instead of the answer.
Look at this chart paper record of a discussion:
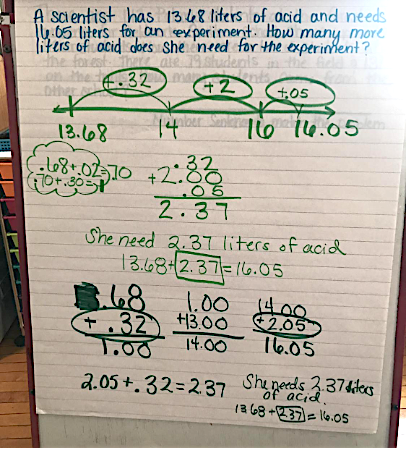
Students share their various reasoning, and the teacher scribes to create an anchor chart to refer back to during the discussion and later, when we tackle other problems.
#2 – Choose who shares strategically. Select students who have clear reasoning to share. Do not wait to select students with their hands up or those that are willing to share. Instead, use work time to find the students with strong reasoning that offer something for others to learn from. Then ask them to share. This approach will help you structure the math discussion to work toward a deeper understanding for the class, rooted in students’ reasoning. Over time you’ll have more and more students to choose from.
#3 – Make explicit what you mean by “show your reasoning.” Give students a model for what it looks like to show reasoning. My favorite way to do that is by sharing CAP – Clear, Accurate, Precise. Discuss what each word means and then how it applies to mathematical reasoning. As you look at an example piece of work and ask questions to discuss, it might sound like this:
What would it look like for this work to be clear?
What makes this reasoning accurate?
How is this diagram precise?
What could be added to make this more precise?
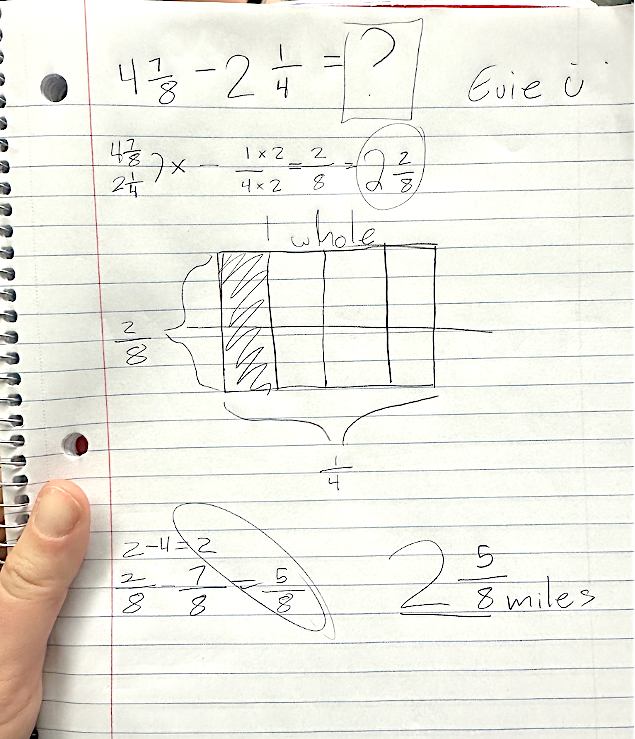5th grader’s reasoning for the problem: Leo walked 4 7/8 miles last week and 2 1/4 miles this week. How much more does he need to walk to match last week’s distance?
Redefining Our Beliefs
Helping students show their reasoning isn’t about adding one more step; it’s about redefining how we believe math learning happens. At the heart of this work is the belief that students learn not through memorizing steps, but through reasoning, discussion, and exploration. When we believe in the process, center students’ voices, and trust students’ brilliance, we create classrooms where students see their thinking as the most important part of doing mathematics.
The strategies for helping students engage in real-world problems don’t depend on a certain curriculum or set of standards, but instead rest on the belief that children learn through curiosity and exploration of mathematics. They learn through sharing and discussing their ideas with peers, through strategic guidance and nudges from teachers.
If this is the kind of classroom culture you’re building, you’ll find practical tools and encouragement inside my first book, Word Problem Workshop, releasing in the fall.
Mona Iehl is an elementary and intermediate educator who transformed her approach to teaching math by embracing student-centered methods that foster curiosity and engagement. She has captured her process in her new book, Word Problem Workshop: 5 Steps to Creating a Classroom of Problem Solvers (Routledge/Stenhouse, October 2025), available for pre-order. Mona now coaches educators to create inclusive math classrooms where all students develop deep, lasting problem-solving skills. Follow her Math Chat Podcast and connect with her online @HelloMonaMath.
